Схема колесной нагрузки принимается той же, что и при определении наибольшей величины эквивалентной нагрузки (рисунок 1.5)
Рисунок 1.5 – Схема расчёта напряжений по основной площадке земляного полотна
Напряжения на основной площадке земляного полотна σh на глубине h определяются под расчетной шпалой с учетом давлений, предаваеимых двумя соседними шпалами по формуле
, (1.35)
где σh0 – напряжения от действия расчетной шпалы на глубине hот её подошвы;
σh1,σh2 – напряжения от действия соседних шпал.
Определим напряжение от расчетной шпалы:
, (1.36)
где r1 – параметр, учитывающий влияние материала шпал на напряжения (для железобетонных шпал r1 = 0,7);
m1 – коэффициент учитывающий неравномерность напряжений по ширине подошвы шпалы и определяемый как
, (1.37)
C1 и С2 – константы зависящие от геометрии шпального основания (ширины подошвы шпалы b, м, толщины балласта h, м, расстояния между осями шпал lш, м), определяемые по формулам
, (1.38)
, (1.39)
;
;
;
МПа
Определим напряжения от соседних шпал
Для определения напряжений под соседними шпалами найдем давление на эти шпалы с помощью линий влияния прогибов в соответствии с установкой колёсной нагрузки. Для установки, показанной на рисунке 1.5, давления на соседние шпалы определяются по формулам
,(1.40)
, (1.41)
l1–lш = l2 – lш = 2,15 – 0,5 = 1,65м;
l1+ lш = l2+lш = 2,15 + 0,5 = 2,65м;
;
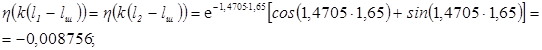
Напряжения в балласте под соседними шпалами находятся по формулам
; (1.42)
МПа;
Нормальные вертикальные напряжения на глубине hот расчётных давлений под подошвами шпал определяются по формулам
; (1.43)
, (1.44)
где Ah – константа, зависящая от геометрии шпального основания определяемая по формуле
;(1.45)
где β1 и β2 – углы, характеризующие геометрию подрельсового основания
; (1.46)
рад;
; (1.47)
рад;
;
МПа.